Monte Carlo 방법의 수학적 기초
참고
- 해당 글은 Scratchpixel의 Monte Carlo Simulation 글 중심으로 작성되었다는 것을 밝힙니다.
1. Monte Carlo, Biased and Unbiased Ray Tracing
Monte Carlo Ray tracing에는 두가지 수식어가 존재한다. biased와 unbiased이다.
먼저, 카메라를 통해 찍은 이미지가 있고 물체에서 반사된 빛은 격자(pixels)에 보여질 것이다. 이 빛은 결국 하나의 color로 바뀔 것이다. 그러나, 이러한 pixel들은 점이 아니라 작은 면적(small surface)이라, 그 안에 여러 물체 또는 여러 색이 동시에 들어 올 수 있다. 따라서 픽셀 당 단일 색을 얻으려면, 픽셀 면적 전체에서 들어오는 빛을 평균을 내야하는 것이다.
\[L_{pixel} = \int_{pixelarea}L(x_p)dA \tag{1}\]하지만, 이 계산은 전형적인 계산불가능한 문제이다. 따라서 우리는 수학적으로 $(1)$수식으로부터 해답을 구할 수 없다. 따라서, 해석적 해가 존재하지 않으므로, 수치적 근사(numerical approximation)이 필요하다. 원리는 매우 간단한데, pixel 표면에 대해서 N개의 랜덤 샘플링을 수행함으로써 근사하는 것이다.
\[L_{pixel} \approx \frac{1}{N}\sum^N_{n=1}L(x_n) \tag{2}\]이 방법을 Monte Carlo integration이라고 부른다.
샘플 개수가 많을 수록 서로 평균이 비슷해지므로, 색이 비슷해진다는 것을 알 수 있다. 렌더링하는 과정에서 이러한 차이는 noise(assuming you are using a ray tracer)라고 불린다. noise는 실제 값과 근사치 사이의 차이에서 비롯되며, 통계학적으로는 variance라고 부른다.
하지만, 같은 샘플 수를 쓰더라도 근사값들의 차이가 발생한다. 이는 같은 세팅에서의 렌더링 결과들이 들쑥날쑥하다고 해석할 수 있다.
Monte Carlo 적분을 레이 트레이싱으로 수행하기 때문에 이 방법을 Monte Carlo Ray Tracing 또는 Stochastic Ray Tracing이라 부른다. (‘Stochastic’은 ‘무작위’라는 뜻이다.) 아래의 논문들이 이 토대를 세웠다고 한다.
- The Rendering Equation (Kajiya, 1986)
- Stochastic Sampling in Computer Graphics (Cook, 1986)
- Distributed Ray Tracing (Cook, Porter, Carpenter, 1984)
1.1. Biased and Unbiased
통계학적으로, 기대값 $E(X)$를 근사하는 규칙을 estimator라고 한다.
\[Approximation((E(X))=\frac{1}{N}\sum^N_{n=1}x_n \tag{3}\](3)공식이 estimator의 예시 중 하나이다. estimator가 unbiased하다는 것은 샘플 수 $N$을 무한히 늘리면 그 결과가 실제 기대값에 수렴하는 의미이다. Monte Carlo Estimator는 이 조건을 만족한다.
반대로, $N \rightarrow \infty$일 때도 결과가 기대값으로 수렴하지 않는다면 bias가 있다고 말한다. 이렇게 biased된 estimator는 어떤 값으로 수렴하게 될텐데, 다음과 같은 장점이 존재한다.
- 편향이 매우 작으면서 수렴 속도가 빠르다.
- 같은 샘플 수에서 variance(noise)가 적다.
위의 장점들을 다시 적어보면, biased estimator는 여러 번 근사치를 계산하여도, 매 번 결과가 크게 흔들리지 않아 이미지 노이즈가 줄어드는 효과를 얻을 수 있다라는 것이다. 잊지 말아야 할점은 unbiased MC와 비교하여 biased MC는 ‘true’ 결과값가 차이가 존재하는 것이다.
1.2. Extend the concept to Shading
우리는 카메라로부터 발사한 Ray가 교차하는 점인 $P$가 반구(hemisphere)형태 받아들이는 빛의 양을 계산해야한다.
\[L_P = \int_\Omega L_\Omega \approx \frac{1}{N}\sum^N_{n=1}L(x_n) \tag{4}\]하지만, 여기서 적분을 풀 방법이 없으므로 다시 한번 Monte Carlo 적분을 사용한다. 반구 표면에 무작위 샘플을 찍고, 각 방향으로 $P$에서 Ray를 발사해 그 방향에서 들어오는 빛을 측정해 평균을 내서 근사하는 것이다.
그림3처럼 점 $P$에 도달하는 빛을 계산하기 위해 재귀적으로 동작한다. 그리고, 계산하기 위해 $P$에서 쏜 $Ray$가 다른 물체와 교차하면, 그 지점에서도 같은 방법으로 빛을 근사한다. 이렇게 재귀적으로 반복되며, 이런 이유로 이 알고리듬을 Path Tracing이라고 부르는 것이다.
1.3. PMF, PDF, CDF
PMF(Probability Mass Function)는 이산적 확률 분포로 $Pr=[0.5, 0.2, 0.3]$과 같은 식을 이야기한다. PDF(Probability Distribution Function)은 이산적이지 않고 연속적인 확률 분포를 이야기한다. PDF 전체 영역을 적분하면 반드시 1이 된다.
CDF(Cumulative Distribution Function)은 CG분야에서 Monte Carlo 방법을 사용할 때 가장 중요한 개념 중 하나이다. CG에서 렌더링할 때 수많은 적분이 등장하는데, 이를 효율적으로 계산하기 위해 Inverse Sampling Method(역변환 샘플링)라는 방법을 쓰며, 이 방법이 CDF에 기반하기 때문이다.
고등학교 적분을 배울 때 리만 합(Riemann sum)이라는 기법을 배웠을 것이다. 적분 구간을 일정 간격으로 나누어 함수 값을 평가한 뒤, 그 값에 구간 폭(두 구간 사이의 거리)을 곱하고 모두 더한다. 두 샘플의 간격이 작아질수록 근사치는 더 정확해지는 것이다.
그림 4를 예시로 들면, 실제 확률의 합을 구하는 적분 구간은 $[-\infty, \infty]$이지만, 함수 값이 구간 $[-5, 5]$ 밖에서는 거의 0이므로 그 범위만 고려해도 무방하다.
| 샘플 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | -4.5 | -3.5 | -2.5 | -1.5 | -0.5 | 0.5 | 1.5 | 2.5 | 3.5 | 4.5 |
| g(x) | 0.000 | 0.000 | 0.017 | 0.129 | 0.352 | 0.352 | 0.129 | 0.017 | 0.000 | 0.000 |
위의 표는 실제로 10개 샘플에 대한 PDF 결과이다. 각 값에 샘플 간 거리(dx=1)를 곱해 모두 더하면 1이 된다는 것을 알 수 있다. 샘플이 적으면 리만 합을 통해 얻은 값이 1에 가까운 값을 주지만, 샘플 수를 늘릴수록 합은 1에 점점 수렴한다.
여기서 리만합을 언급한 이유는 특정 구간을 샘플링해서 적분한 결과가 1에 수렴한다면 거기가 기여도가 많다는 것이다. PDF가 중요한 이유는, 광선 방향, 광원 위치 등 고차원 적분을 낮은 분산으로 근사하려면, 실제 기여량에 비례하는 PDF가 필요하기 때문이다.
확률 이론에서 CDF는 “랜덤 변수 $X$가 처음 $N$개의 가능한 값 중 하나일 확률”과 같은 계산에 유용하다. 예를 들어, 주사위에서 4 이하 숫자가 나올 확류을 알고 싶다면 1, 2, 3, 4가 나올 확률을 모두 더하면 된다.
이걸 연속확률분포에도 적용해보면, $X$가 0이하 값을 가질 확률은 $X<=0$ 의 범위의 확률을 모두 더하면 되는 것이다. 그림 5에서 파란 곡선을 통해 확인할 수 있다.
1.4. Low of the unconscious statistician(무의식적인 통계학자의 법칙)
$X$라는 값이 존재하고, $F(X)$라는 함수가 존재한다고 가정하자. 여기서 $E(F(X))$을 구하고자 한다. 가장 먼저 떠오르는 방법은 아래 수식 처럼 $F(X)$를 값을 통해서 확률을 도출해내는 것이다.
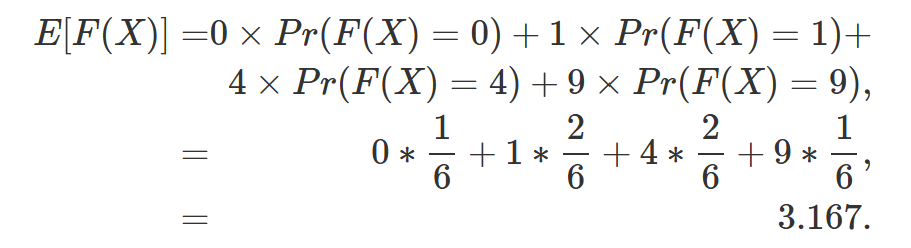
수학적으로 정리해서 쓴다면 (5)와 같을 것이다. 근데, 만약 우리가 $F(X)$의 확률분포를 모른다면 어떻게 해야할까?
\[E[F(X)] = E[Y] = \sum Y_iP_Y(Y_i) \tag{5}\]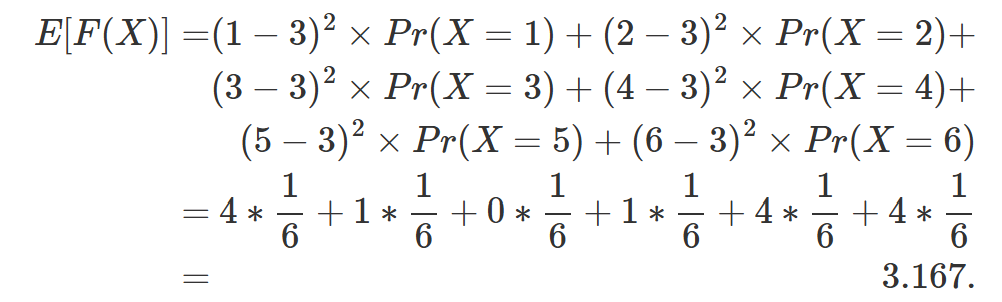
재료가 되는 $X$의 확률 분포만 안다면, 우리는 함수를 통해서 값이 바뀌어도 $F(X)$의 기댓값을 충분히 구할 수 있다. 현재 수식은 이산적인 변수에만 적용되지만, 이걸 연속적으로 바꾼다면 아래와 같다.
\[E[F(X)] = E[Y] = \int F(X)P_X(X)dX \tag{7}\]이것은 무의식적인 통계학자의 법칙이라고 불린다. 우리는 변한 값들의 분포에 대해서 몰라도 원본 값으로 충분히 문제를 해결할 수 있는 것이다. 즉, 두 번 계산하지 않아도 된다.
2. Inverse Transform Sampling Method
앞서 설명해듯이, CDF는 어떤 연속적인 랜덤 변수 $X$에 대해서 $X<=?$를 모두 더하는 것으로 확률을 구할 수 있다.
C++에서 drand48()함수를 사용하면, [0, 1]사이의 값을 균등하게 뽑아준다. 만약, 여기에 CDF의 개념을 도입하면, CDF는 0에서 1까지 단조 증가하므로, drand48()의 결과 값인 $r$이 CDF의 값이라고 말할 수 있다.
직관적으로 [0, 1]사이의 값을 균등하게 뽑아내고 확률적인 입장에서 1에 가까울수록 확률이 높다. 예를 들어, 0.8이 나올 확률은 0.1씩 격자를 쪼갠다고 했을때, [0.1, 0.8]까지의 확률의 합이고 이는 0.8이랑 같다는 것을 알 수 있다.
핵심은 균등 난수 $r$을 CDF의 결과 값으로 보고 역함수를 전개해보자.
\[x = InvCDF(r) \tag{9}\](8)에서 확인할 수 있듯이, $x$를 추출할 수 있는데, 이것이 원하는 PDF(왜냐하면, CDF는 PDF로부터 파생되기 때문이다.)를 따르는 난수가 된다는 점이다. 즉, 균등 난수(uniform variable)만으로 어떤 분포든 샘플링할 수 있게 해주는 것이 역변환 샘플링 기법이다.
핵심을 요약하면 아래와 같다.
- 우리가 시뮬레이션 하길 원하는 연속확률분포인 $PDF\ p(x)$가 있다.
- $PDF\ p(x)$를 이용해서 $CDF\ F(x)$를 계산한다.
- 특정한 방법을 통해 $InvCDF\ F^{-1}(x)$를 계산한다.
- 균일한 분포(uniform distribution)로부터 균등 난수 $\epsilon$을 추출한다.
- $x = F^{-1}(r) \rightarrow \ x \sim p(x)$를 구할 수 있다.
글로 한번 더 요약하면, 우리가 알고 있는 어떤 연속확률분포(PDF)인 p(x)가 있고, p(x)를 따르는 어떤 값 x를 추출하고 싶은 상황이다. 근데, 분포를 아는 것과 분포에서 샘플링하는 것은 다른 문제이다. 그러므로, $InvCDF(r)$를 이용해서 샘플링을 진행하는 것이다.
2.1. how do we find the invert of the CDF?
몇몇 케이스에 대해서 역변환 CDF에 대한 형태가 존재한다. 하지만, 그렇지 않은 케이스도 존재한다. 그러므로, 우리는 범용적인 솔루션을 얻을 필요가 있다. 해결책은 **PDF를 disretize하는 것이다. 앞에서 설명했듯이, PDF를 일정 간격으로 샘플링한 뒤 리만 합으로 누적하면 대응되는 CDF를 쉽게 만들 수 있다.
//https://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/monte-carlo-methods-mathematical-foundations/inverse-transform-sampling-method.html
// standard normal distribution function
float pdf(const float &x)
{ return 1 / sqrtf(2 * M_PI) * exp(-x * x * 0.5); }
int main(int argc, char ** argv)
{
int nbins = 32;
float minBound = -5, maxBound = 5;
float cdf[nsamples + 1], dx = (maxBound - minBound) / nbins, sum = 0;
cdf[0] = 0.f;
for (int n = 1; n < nbins; ++n) {
float x = minBound + (maxBound - minBound) * (n / (float)(nbins));
float pdf_x = pdf(x) * dx;
cdf[n] = cdf[n - 1] + pdf_x;
sum += pdf_x;
}
cdf[nbins] = 1;
printf("sum %f\n", sum);
for (int n = 0; n < nsamples + 1; ++n) {
printf("%f %f\n", minBound + (maxBound - minBound) * (n / (float)(nbins)), cdf[n]);
}
...
return 0;
}
위 코드를 통해 CDF를 만들 때 주의해야할 점은 반드시, 시작과 끝이 0과 1이 되어야만 한다는 것이다. 비록 이산화된 PDF를 이용하여 CDF를 만들었지만, CDF 자체는 여전히 연속 함수이다.
CDF를 만들었지만, 중간중간 빈 지점들은 선형증가한다고 보면 된다. 균등 난수 $r$을 통해서 어떤 지점인지 확인을 해야한다. 여기서는 비례식을 이용한다.
CDF는 $0 \rightarrow 1$로 단조 증가하는 분포이고, 우리는 여기서 n=15와 n=16 사이에서 $r$이 얼마나(t) 안쪽에 위치해 있는지 알고 싶다.
직선 방정식을 통해 선형 근사하는 방법도 존재한다. 다만, 비례식을 이용해서도 값을 구할 수 도 있다.
\[y = y_0 + \frac{y_1 - y_0}{x_1 - x_0}(x-x_0) \tag{11}\] \[t = DE = \frac{(r-lower\ bound)}{(upper\ bound-lower\ bound)} \tag{12}\]선형 보간 비율인 t를 위와 같이 구할 수 있다. 그리고 전체비율이니까, $AC=1$이라고 생각하자.
\[\frac{DE}{AB}=\frac{DF}{AC}=\frac{t}{1}=\frac{DF}{dx} \tag{13}\]그러면, $DF = t \times dx$라는 식이 나온다는 것을 확인할 수 있다. 그러면 우리는 마침내 $x$를 찾을 수 있게 된다. min은 전체 구간의 왼쪽 끝을 의미하고 off는 왼쪽 끝으로부터 몇 번째 셀인지를 의미한다.
\[x = min + n_{lower}*dx + DF =min +(n_{lower}(off) + t) * dx \tag{14}\]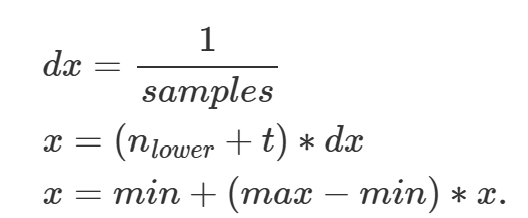
위 식과 같이 해당 계산을 통해 구한 x에 대해서 원래 실수 구간 [min, max]로 스케일을 돌려주는 과정이다. 이 과정을 통해 풀게되면, 역변환 CDF를 구하는 것 없이 균등 난수를 원하는 PDF 범위의 난수로 변환할 수 있다.
« Meshlet Rendering using Vulkan
Monte Carlo Simulation »