Ray Tracing

위 포스팅은 아래와 같은 자료들을 참고하였습니다.

• CSE 168 - Computer Graphics II-Rendering(UCSD)

• Model → World → View coordinates

1. Ray tracing

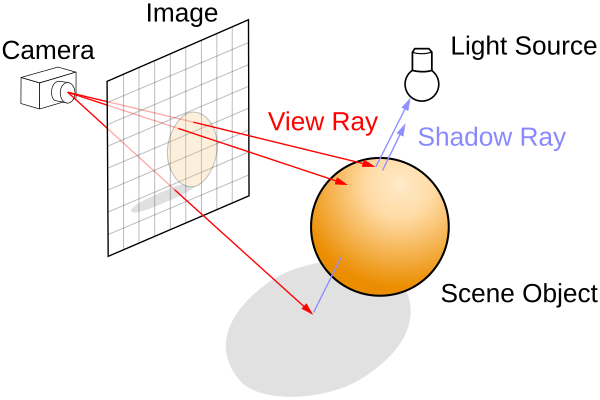
• Generating an image by tracing the path of light through pixels.
• Higher degree of visual relism

view ray를 발사하게 되면, scene object의 표면에 닿는 지점이 발생한다. 해당 지점이 받아들이는 빛의 양을 계산해서 실사와 같은 이미지를 만들어내는 원리이다.

이때, 표면 재질에 따라 빛을 흡수할 수도 있고 빛의 반사되는 방향이 달라질 수 있다. 이러한 성질을 정의한 것이 BSDF 라고 한다.

1-1. Intersection with sphere

\[Ray:\ \vec{p}(t) = \vec{e} +t\vec{d} \tag{1}\] \[Sphere:\ (x-x_c)^2+(y-y_c)^2+(z-z_c)^2-R^2=0 \tag{2} \\ (\vec{p}-\vec{c})\cdot(\vec{p}-\vec{c})-R^2 = 0\]

광선과 구의 방정식은 (1)번과 (2)번식처럼 정의할 수 있다. $\vec{p}$에다가 Ray의 식을 넣어서 정리해보자.

\[(\vec{d}\cdot\vec{d})t^2+2\vec{d}\cdot(\vec{e}-\vec{c})t+(\vec{e}-\vec{c})\cdot(\vec{e}-\vec{c})-R^2=0\ \ \ \ \ \ \tag{3}\]

위의 식을 $t$에 관한 2차식이라고 가정할 때, 판별식(discriminant) 을 이용할 수 있다. $d= \sqrt{b^2-4ac}$ 라는 간단한 식을 통해 해가 몇 개 존재하는지 파악할 수 있다.

판별식은 근의 공식에서 도출된 만큼, $t0$과 $t1$이 근의 공식의 해인 것이다.

• $d > 0$: 서로 다른 두 개의 실근을 갖게 된다. (intersection)
• $d=0$: 하나의 중근을 갖게 된다. ($t0=t1)$
• $d<0$: 서로 다른 두개의 허근을 갖게 된다. (no intersection)

이미지에서 볼 수 있듯이, 중요한 점은 ray origin의 위치가 어디있는가에 따라 다르다는 점이다. $d>0$이라고 하여도, 실제로 구한 해의 값에 따라 $e$(ray origin)의 위치가 3가지 경우의 수가 존재하고 $t0$과 $t1$의 값을 통해 어느정도 위치를 유추할 수 있다.

1-2. Intersection with triangle

\[Normal:\ \vec{n}=\frac{(C-A)\times(B-A)}{|(C-A)\times(B-A)|} \tag{4}\] \[Plane:\ (\vec{P}-\vec{A})\cdot{\vec{n}}=0 \tag{5}\]

Normal이란, 삼각형의 앞면/뒷면을 결정짓는 요소이다. 그렇기 때문에 cross product 를 통해서, 삼각형의 면이 어느 면을 바라보고 있는지 계산하는 것이다. 그리고 normal vector는 기본적으로 unit vector이기 때문에 정규화를 해주는 모습을 볼 수 있다.

여기서, 중요한 특징은 1차 방정식을 이용한다는 점이다. ray와 sphere의 경우에는 sphere 표면의 휘어짐이 존재하기 때문에 2차 방정식을 이용해야했지만, 삼각형의 경우에는 일차원적인 평면이기 때문에 그럴 필요가 없다.

(5)번식을 풀어보면 평면 위에 아무 점 $\vec{A}$를 잡고서 우리가 확인하고 싶은 점 $\vec{P}$이 정말로 평면 위에 있다면, $\vec{P}-\vec{A}$와 $\vec{n}$의 dot product 는 0이 될 수 밖에 없다는 것이다.

\[Ray:\ \vec{P}=\vec{P_0}+t\vec{P_1} \tag{6}\]

광선의 방정식은 언제나 똑같다. 광선의 시작지점 $\vec{P_0}$이 있고 시간에 따라 누적 진행한 거리 $t\vec{P_1}$이 존재한다. 위 광선의 식을 평면 방정식에 대입해보자. (7)번 식을 통해서 우리는 $t$를 구할 수 있다.

\[Intersection:\ t=\frac{\vec{A}\cdot\vec{n}-\vec{P_0}\cdot\vec{n}}{\vec{P_1}\cdot\vec{n}} \tag{7}\]

1-3. Radiance and Irradiance

Radiance

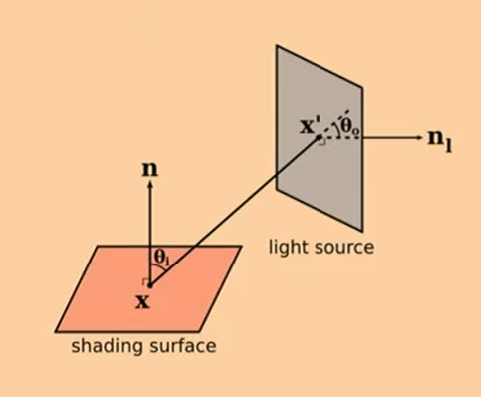
Radiance란 무엇인가? 한국어로 직역하면 ‘방사 휘도’라고 한다. 그림으로 한번 이해해보자. 아래 그림처럼, 한 점에서부터(작은 면적) 나오는 빛의 양을 radiance라고 한다.

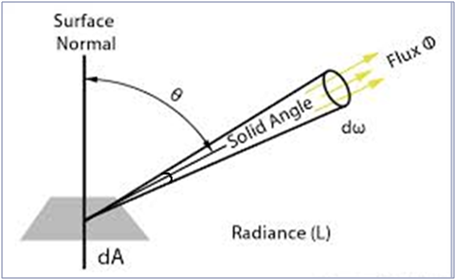
radiance를 정의하기 위해 필요한 파라미터는 총 5개이다. 장애물에 막히지 않는 한 radiance의 값은 일정(constant)하다. 이 특징은 렌더링 공식에서 매우 중요한 역할을 수행한다.

• $L(\overbrace{x, y, z}^{eye}, \overbrace{\theta, \phi}^{lookat})$: Position(3D) + Angle(2D)

즉, 빛이란 중간에 다른 무건가에 부딪히지 않는 한 갖고 있는 에너지가 일정하다는 의미이다. 그렇기 때문에 픽셀의 색상을 계산하는 복잡한 문제를 매우 단순하게 만들어 준다.

• 예를 들어, 점 P에 조명에서 오는 빛이 얼마나 영향을 주는지 계산하고 싶다고 해보자.
• ‘Radiance는 막히지 않는 한 일정하다’는 속성을 사용합니다. 만약 광선 중간에 다른 물체가 없다면(막히지 않았다면), 조명에서 출발한 Radiance는 손실 없이 그대로 점 P에 도달합니다.
• 만약 중간에 다른 물체가 있다면(막혔다면), 조명에서 오는 Radiance는 0이 됩니다. 이것이 바로 그림자가 생기는 원리입니다.

Irradiance

radiance가 작은 면적으로부터 나오는 빛의 양을 이야기한 것이었다면, irradiance는 ‘한 점(작은 면적)에 들어오는 빛의 합’을 이야기 한다. refraction(굴절)에 의해서 값이 증가하거나 줄어들 수 있다는 특징이 있다.

예를 들어, 볼록 렌즈를 통해 빛을 모으게 된다면 Irradiance는 증가할 것이다. 하지만 radiance는 변하지 않는다. 왜냐하면 각 빛의 양은 모두 일정하기 때문이다.

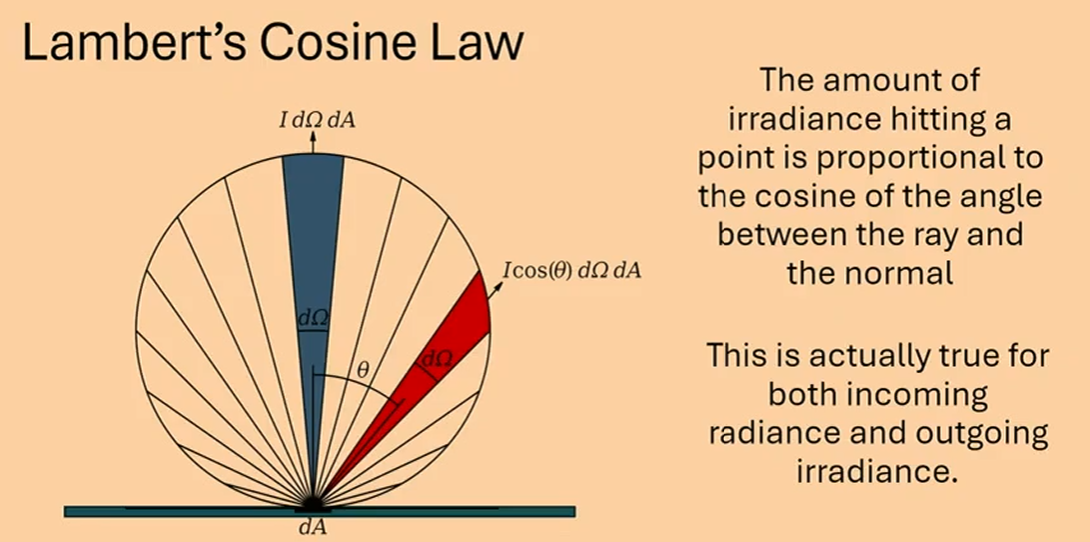
• ‘표면이 어떻게 빛을 반사하는가’에 대한 가장 기본적인 물리 법칙 (Lambert’s Cosine Law)

  바로, 램버트 코사인 법칙 이다. 결국 빛의 양(밝기)이란, 표면의 normal과 빛이 들어오는 방향 사이의 각도$\theta$의 $cos(\theta)$값에 비례한다는 것이다.

  \[E(x) = \int dw_i L(w_i)cos(\theta) \\ = \int dw_i L(w_i)(\vec{n}\cdot\vec{w_i})\]

Material Emission and BSDF

→ (오타) BRDF: ratio of incoming irradiance to outgoing irradiance (x)

→ (정정) BRDF: ratio of incoming irradiance to outgoing radiance (o)

BRDF에 대해서 간략하게 설명해보면, 물체의 표면에 대한 정의이다. 위 이미지는 들어온 빛(irradiance)가 물질의 규칙(=BRDF)를 거쳐서 방향 별로 어떻게 재분배되는지를 표식화한 것이다.

수학적으로 BRDF는 들어온 빛의 양(irradiance)을 분모로 하고 나가는(outgoing) 빛의 양(radiance)를 분자로 해서 최종적으로 irradiance가 radiance로 바뀌는 정도(변환율)를 나타낸다고 볼 수 있다.

그러면, ‘이 변환율이 반사되는 비율이냐?’라고 묻는다면, 답은 ‘아니다’이다. BRDF 자체는 비율이 아니라 미분적 변환율이고 BRDF를 적분해야 직관적으로 말하는 ‘반사되는 비율’이 되는 것이다.

\[\rho_{dh}(x,w_i)=\int_\Omega f_r(x, w_i, w_o) cos(\theta_o) dw_o \leq 1 \tag{8}\]

(8)번 식에서 간혹 $dw_o$이 아닌 $dw_i$에 대해서 적분하는 것을 볼 수 있을 것이다. 그 이유는 directional-hemispherical reflectance 와 hemispherical-directional reflectance 의 차이다.

• $dh$: 입사 방향 $w_i$를 고정하고 출사 반구 전체로 퍼져 나가는 양을 모두 합친 비율이다 → ‘이 방향에서 들어온 빛이 총 얼만큼 반사되었나?’
  • 입사가 directional → 출사가 hemispherical ⇒ $ω_o$로 적분
• $hd$: 출사 방향 $w_o$를 고정하고 입사 반구 전체에서 들어오는 빛을 합친뒤 나가는 비율이다 → ‘전체적으로 조명을 비추었을 때, 이 방향으로 얼마나 밝게 보이는가?’
  • 입사가 hemispherical → 출사가 directional ⇒ $ω_i$로 적분

결국 우리가 렌더링을 통해서 구해야 할 것은 화면에 있는 픽셀로부터 해당 물체의 표면이 얼마나 밝게 보이는가에 대해서 알아야하므로, 쓰이는 식은 $hd$기반이다.

• 그러면, 계산은 어떠한 순서로 이루어질 것인가?
  1. 화면의 픽셀에서 Ray를 발사한다.
  2. 발사한 Ray이 물체의 표면($x$)이 닿는다.
  3. 닿은 물체의 표면에 대해서, 중요도 샘플링(BSDF, MIS)을 통해 또 다른 Ray $\omega_i$들을 발사한다.
  4. 화면의 픽셀로 나가는 빛의 양을 $L_o(x, w_o)$을 재귀(Recursion)로 추측하는데, 이때 $L(\omega_i)$들을 계산한다. 여기서 $w_o$란, 화면의 픽셀로 나가는 방향을 의미한다.

  즉, 추측하고자 하는 값은 화면의 픽셀로 나가는 빛의 양이다. 재귀로 추측하는 이유는 적분을 풀지 못하는 문제이기 때문이다.

1-4. How it is calculated?

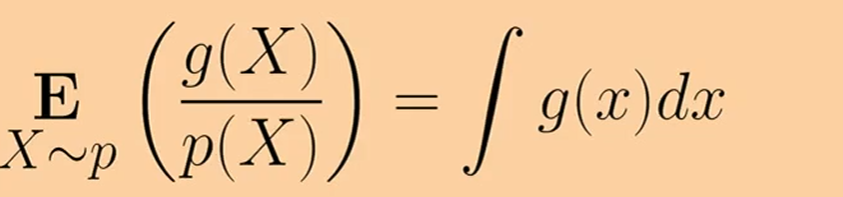
위에서 언급한 내용들을 수식으로 정리한 것이다. ‘적분→기댓값 $E$’으로 바꾸어서, 표본 평균을 추정하자는 설명이다.

$U$는 uniform distribution 을 의미한다. 일반적인 분포인 $p$라면, 두번째 식처럼 함수에 PDF를 곱해 적분한 것이라고 볼 수 있다.

(중요) 왜 PDF $p$를 통해서 샘플링하는 것인가?

세번째 식도 마찬가지로, PDF $p$로부터 $X$를 뽑아 기댓값을 구한다.

다만 다른 점은 평균을 구하는 식인데, $\frac{g(X)}{p(X)}$의 기댓값을 구하는 것을 볼 수 있다. 이는 구하고자 하는 $g(x)$의 적분을 직접 균등 샘플링하면 노이즈가 클 수 있어, 적은 샘플만 뽑아서 분산이 상대적으로 적은 $p$를 이용해 샘플 $X$를 만들어서 값을 구하는 것이다.

이때, 기댓값을 구하기 위해서 사용되는 방식이 바로 Monte Carlo 인 것이다. 균등 난수를 통해서 PDF $p$에서 샘플 $\omega_i$를 뽑는 방식은 이전 포스팅에서 다루고 있다.

Bias and Variance

1-5. how we reduce Variance?

• 1. Importance Samlping
     • 오해하지 말아야 할 것은 MIS;Multiple Importance Sampling(≠ Important Sampling)란 기법이 있다.

     해당 기법은 광선에 대한 경로를 최적화하는 것이 아니라, 샘플러를 통해 나온 경로들에 대한 값을 중요도를 고려하여 어느 샘플러의 비중을 강하게 하는 것이 분산이 좋을까? 고민하는 기법이다.

  • Direct Lighting의 경우에는 NEE를 사용하지 않는가? 굳이, PDF를 통한 샘플링이 필요한가?

    YES, 왜냐하면 NEE는 ‘광원을 향해 한 번 연결해 보자’라는 샘플링 전략이고 여전히 우리는 광원에 대해서 ‘광원 위의 어느 점(혹은 어느 방향)을 어떻게 뽑았는지’에 대한 문제를 해결해야 한다.

    이는 향후 광원이 많아지면, 어느 광원을 뽑았는지도 분산을 줄이는데에 중요하기 때문에 PDF를 통해 샘플링하는 것의 중요성이 부각된다.

• 1. Stratified Sampling

  

  영역 $\Omega$을 겹치지 않는 H개의 층(strata)로 나누고 각 층마다 독립적으로 샘플을 뽑아 평균을 합칩니다. 층 내부 변동은 작아지므로 전체 분산이 감소한다.

• 1. Measure Change