Acceleration Data Structures with NORI
2025/11/19 written. 2025/11/22 updated.
Reference
pbrt v3, https://www.pbrt.org/
NORI, a educational ray tracer
0. Summary
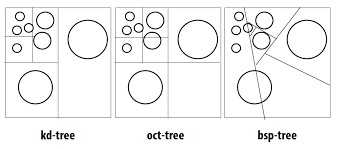
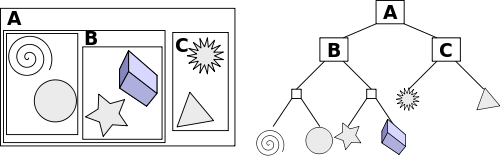
In this post, we consider only three structures, such as, oct-tree, kd-tree and BVH. We classify them into spatial subdivision(oct-tree, kd-tree) and primitive subdivision(BVH). The above pictures show another difference. That is, in spatial subdivisions we have disjoint sets of space regions or voxels or cells whatever you want to call them. In contrast, BVHs have disjoint sets of primitives.
Spatial subdivision approach is some problem that a triangle may overlap multiple spatial regions and thus may be tested for intersection multiple times as the ray passes. But, one property of primitive subdivision is each primitive appears in the hierarchy only once.
We do not consider parallel computing of Acceleration Data Structures. Because It’s the next step. Thus, All rendering time data is computed by single CPU.
1. Octree
First, we talk about the theory of Octree. An Octree is the data structure that implements 3D spatial partitioning to significantly accelerate operations such as ray intersection.
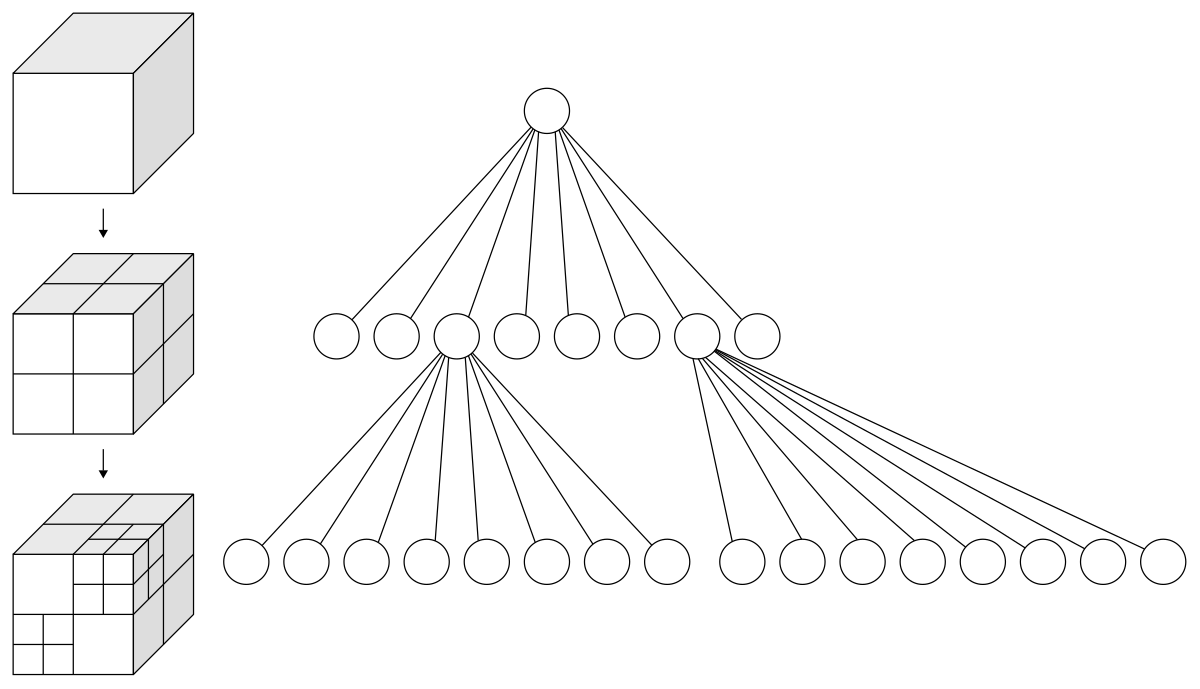
An octree has the parent node that is subdivided into eight children. Each of the children has leaves(e.g. triangles). How octree subdivide a 3d space recursively?, suppose we have a bounding box(e.g. AABB) of object and this bounding box is uniformly! subdivided into eight smaller cubes.
struct Node {
BoundingBox3f bbox;
std::vector<uint32_t> triangles;
std::unique_ptr<Node> children[8];
bool isLeaf() const {
for (int i = 0; i < 8; ++i) {
if (children[i] != nullptr)
return false;
}
return true;
}
};
We can check whether triangle belongs to one of the eight sub-boxes. If the triangle belongs to second sub-box, we add the leaf(triangle) to second sub-box. Recursively, we get into second sub-box. Once again, this bounding box is uniformly subdivided into eight smaller cubes. The leaves of second sub-box are re-distributed to new eight smaller cubes.
void Octree::buildNode(Node* node,
const std::vector<uint32_t>& tris,
int depth) {
// 1. condition of leaf
if ((int)tris.size() <= m_maxLeafTris || depth >= m_maxDepth) {
node->tris = tris;
return;
}
// 2. subdivide the cubes
subdivideNode(node, tris, depth);
}
void Octree::subdivideNode(Node* node,
const std::vector<uint32_t>& triangles,
int depth) {
... // this part make the uniformly eight cubes using node that has an bbox.
BoundingBox3f childBBox[8];
std::vector<uint32_t> childTriangles[8];
for (uint32_t f : triangles) {
const BoundingBox3f& tb = m_triangleBBoxes[f];
for (int i = 0; i < 8; ++i) {
if (cell[i].overlaps(tb)) {
childTriangles[i].push_back(f);
if (childBBox[i].isValid())
childBBox[i].expandBy(tb); // (min, max) of bbox is exapanded from tb to new tb.
else
childBBox[i] = tb;
}
}
}
node->triangles.clear();
for (int i = 0; i < 8; ++i) {
if (!childTris[i].empty()) {
node->children[i] = std::make_unique<Node>();
node->children[i]->bbox = childBBox[i];
buildNode(node->children[i].get(), childTriangles[i], depth + 1);
}
}
This process repeats until a certain condition is met, such as, the node reaches the maximum depth or the number of triangles in the cube is below threshold.
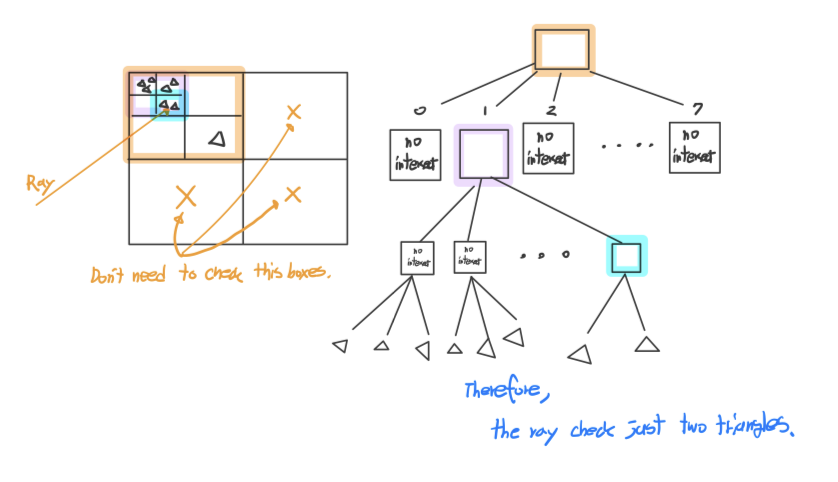We can use this approach for checking ray-intersection between triangle and ray. Suppose you shoot a ray. A naive approach is a ray checks all triangles, however, octree based approach is a ray does not check all triangle. This approach accelerates ray traversal by allowing the ray to only visit the bounding boxes that it intersects.
As a result, a naive approach has $O(N)$. octree based approach has $O(logN)$, but the worst case scenario has $O(log N + N) = O(N)$.
| Maximum Depth (Maximum leaves=8) |
Second |
|---|---|
| 4 | 4.7s |
| 6 | 1.3s |
| 8 | 0.772s |
We can know that the larger the octree has maximum depth, the more space that is not intersected with ray can be skipped, which accelerates culling performance. However, the more memory will be taken.
2. Background
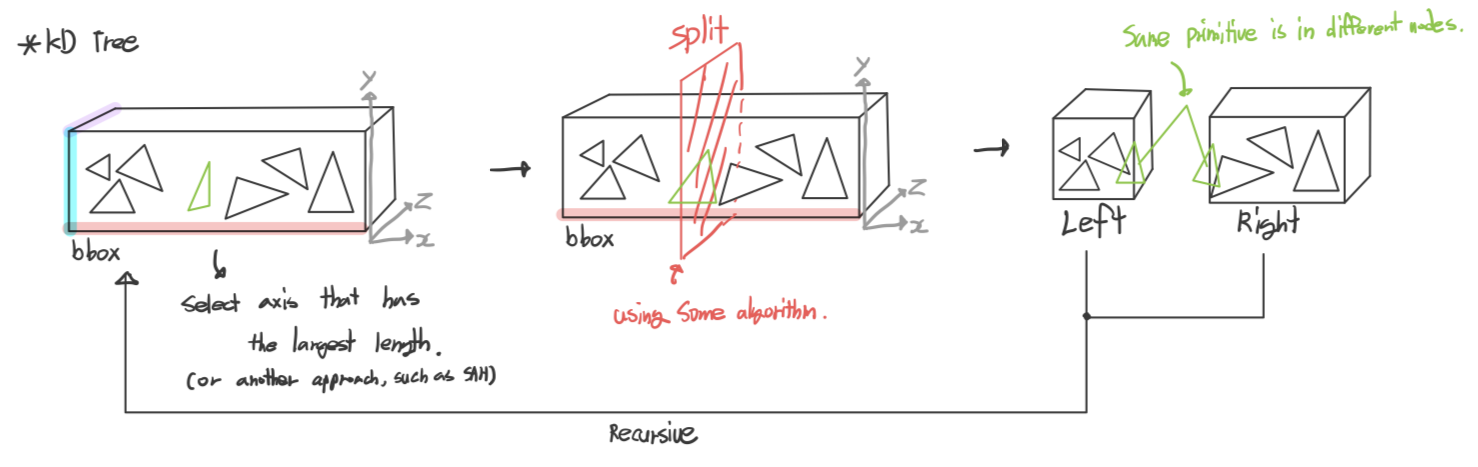
Before we start studying KD Tree and BVH(Bounding Volume Hierarchy), we know how they split the bounding box. Typically, there are two approaches. First, we find the longest axis of the bounding box. Second, we find the lowest cost of ray traversal and ray intersection.
All methods basically want to be subdivided more efficiently from the parent bounding box to left and right children
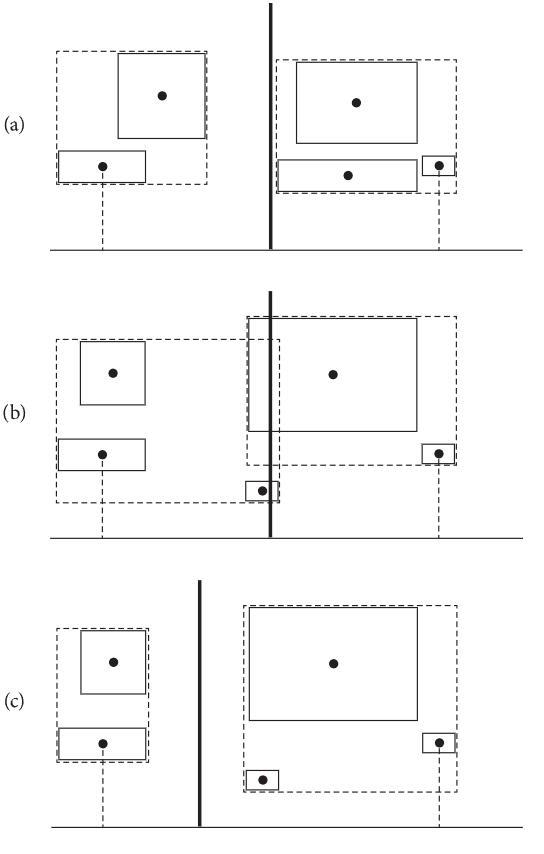
The first method is naive approach. We just find the longest axis to split the bounding box. This approach of splitting is based on the underlying assumption that it leads to the most efficient spatial subdivision. Find the longest axis, sort the primitives (use std::nth-element) to find the middle one, and use its position as the pivot to split the parent bounding box into left and right.
The second method is SAH(Surface Area Heuristic). It’s the same approach to split the bounding box into left and right. We have to know how certain bounding boxes has lower cost than the others.
Cost is computed by
\[\begin{align} c(A, B)=t_{trav} + p_A\sum^{N_A}_{i=1}t_{isect}(a_i)+ p_A\sum^{N_B}_{i=1}t_{isect}(b_i). \end{align}\]$a_i$ and $b_i$ are the indices of primitives in the two children nodes. In pbrt, $t_{isect}$ set to 1. Thus, The sum of all $t_{isect}$ is like count of primitives in bucket.
We find the lowest cost as splitting the parent bounding box based on certain bucket. What means bucket?, We divide the axis into equally sized buckets(the above picture shows) and calculate the SAH cost for splitting after each bucket. Then, we select the boundary that yields the lowest cost for the left and right child nodes.
2.1. KD Tree
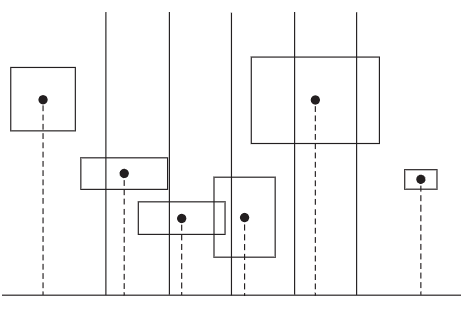
We said kd-tree is spatial subdivision in summary. So, Note that kd-tree can have same primitive in different nodes, but can not have same region in 3d space. Since the primitive lies on both sides of the split boundary, it belongs to both nodes.
void KdTree::buildNode(Node* node,
const std::vector<uint32_t>& tris,
int depth) {
// Get axis and position(x or y or z) of split line.
int axis;
float split;
if (!chooseSplit(triangles, axis, split)) {
// it's impossible to be subdivided.
node->axis = -1;
node->tris = tris;
return;
}
node->axis = axis;
node->split = split;
...
// We just see only one axis that we selected.
// Note that if it intersect a little bit, you add it to that space.
// This part is different from BVHs.
for (uint32_t idx : triangles) {
const BoundingBox3f& tb = m_triangleBBoxes[idx];
// the bounding box of this traingle is intersected with left half-space
if (tb.min[axis] <= split) {
leftTris.push_back(idx);
}
// the bounding box of this traingle is intersected with right half-space
if (tb.max[axis] >= split) {
rightTris.push_back(idx);
}
}
...
node->tris.clear();
node->left = std::make_unique<Node>();
node->right = std::make_unique<Node>();
// Set bbox based on split line.
// left child bbox
{
BoundingBox3f leftBB = node->bbox;
leftBB.max[axis] = split;
node->left->bbox = leftBB;
}
// right child bbox
{
BoundingBox3f rightBB = node->bbox;
rightBB.min[axis] = split;
node->right->bbox = rightBB;
}
buildNode(node->left.get(), leftTris, depth + 1);
buildNode(node->right.get(), rightTris, depth + 1);
The most important thing is how the split line and axis is selected.
// 1. Evaluate bounding box of centeroid.
BoundingBox3f centroidBB;
for (uint32_t idx : tris)
centroidBB.expandBy(m_triCenters[idx]);
Vector3f extents = centroidBB.getExtents(); // length of x, y, z axis
// 2. Select the largest axis.
int axis = 0;
if (extents[1] > extents[axis]) axis = 1;
if (extents[2] > extents[axis]) axis = 2;
...
// We see only center of primitives at the largest axis.
// So, we can get the dim [N, 1]
std::nth_element(centers.begin(),
centers.begin() + centers.size() / 2,
centers.end());
float split = centers[centers.size() / 2];
outAxis = axis;
outSplit = split;
...
The above approach is to select the median of primitives. We can get them to use another approach, SAH.
const int NUM_BINS = 16;
struct Bin {
int count = 0;
BoundingBox3f bbox;
};
float bestCost = std::numeric_limits<float>::infinity();
int bestAxis = -1;
float bestSplit = 0.f;
// We need to find the lowest cost in (x, y, z) axis for building KD-Tree.
for (int axis = 0; axis < 3; ++axis) {
if (extents[axis] <= 0.f)
continue; // This axis don't be subdivided
float minA = nodeBB.min[axis];
float maxA = nodeBB.max[axis];
float invExtent = 1.f / (maxA - minA);
Bin bins[NUM_BINS];
// 1) Each primitive is divided into bin using centroid.
for (uint32_t idx : triangles) {
const Point3f& c = m_triangleCenters[idx];
const BoundingBox3f& tb = m_triangleBBoxes[idx];
float pos = c[axis];
float t = (pos - minA) * invExtent; // [0,1]
int b = (int)(t * NUM_BINS);
if (b < 0) b = 0;
if (b >= NUM_BINS) b = NUM_BINS - 1;
bins[b].count++;
bins[b].bbox.expandBy(tb);
}
...
BoundingBox3f curBB;
int curCount = 0;
for (int i = 0; i < NUM_BINS - 1; ++i) {
curBB.expandBy(bins[i].bbox);
curCount += bins[i].count;
leftBBox[i] = curBB;
leftCount[i] = curCount;
}
curBB = BoundingBox3f();
curCount = 0;
for (int i = NUM_BINS - 1; i > 0; --i) {
curBB.expandBy(bins[i].bbox);
curCount += bins[i].count;
rightBBox[i - 1] = curBB;
rightCount[i - 1] = curCount;
}
// 3) Estimate cost abot each bin boundary
for (int i = 0; i < NUM_BINS - 1; ++i) {
int cL = leftCount[i];
int cR = rightCount[i];
if (cL == 0 || cR == 0)
continue;
float areaL = leftBBox[i].getSurfaceArea();
float areaR = rightBBox[i].getSurfaceArea();
if (areaL <= 0.f || areaR <= 0.f)
continue;
// C = C_trav + (A_L/A_P)*N_L*C_isect + (A_R/A_P)*N_R*C_isect
// We set cost of ray intersect to 1. (It's similar to PBRT)
float cost = 0.125f
+ (areaL / parentArea) * (float)cL
+ (areaR / parentArea) * (float)cR;
if (cost < bestCost) {
bestCost = cost;
bestAxis = axis;
float fraction = (float)(i + 1) / (float)NUM_BINS;
bestSplit = minA + fraction * extents[axis];
}
}
}
if (bestAxis == -1)
return false;
outAxis = bestAxis;
outSplit = bestSplit;
return true;
| Sample Count | Second (Median) |
Second (SAH) |
|---|---|---|
| 64 | 11.5s | 11.0s |
| 96 | 16.8s | 16.3s |
| 128 | 25.1s | 22.3s |
This time refers to the time spent from building tree to rendering object(ajax.obj).
2.2. Bounding volume hierarchy
Remember that the difference between KD-Tree and BVH is primitives overlapping in leaves. Because KD-Tree belong to spatial subdivision and BVH belong to primitive subdivision. We must know the difference of them.
Therefore, the overall part of code is similar to KD-Tree. We just modify a part of how BVHs subdivide the primitives.
// BVH
for (uint32_t idx : triangles) {
const Point3f& c = m_triangleCenters[idx];
if (c[axis] < split)
leftTris.push_back(idx);
else
rightTris.push_back(idx);
}
// KD-Tree
for (uint32_t idx : triangles) {
const BoundingBox3f& tb = m_triangleBBoxes[idx];
// the bounding box of this traingle is intersected with left half-space
if (tb.min[axis] <= split) {
leftTris.push_back(idx);
}
// the bounding box of this traingle is intersected with right half-space
if (tb.max[axis] >= split) {
rightTris.push_back(idx);
}
}
We can see the difference between primitive and space from the above code. As BVH subdivide primitives using center of primitive, the primitive doesn’t be overlapped in leaves. That is, if we make the BVH, we can use the lower memory and make faster to build tree than KD-Tree . Because there is no overlap.
| Sample Count | Second (Median) |
Second (SAH) |
|---|---|---|
| 128 | 1.9s | 1.7s |
| 256 | 3.8s | 3.5s |
| 512 | 7.4s | 6.8s |
We can see it faster than KD-Tree. That’s because BVH didn’t spend many times in building tree. In experiment, we used small object(V=409676, F=544566). Therefore, Maybe they were not evaluated accurately.
« How the direction are sampled from BRDF?